 算法[我的2019版]
算法[我的2019版]
# 稀疏数组
# 概述
下图左侧的含有大量空值的数组可以用稀疏数组来表示, 右侧为稀疏数组。

左侧的为 11x11 的二维数组, 假设为 a。 数组中有两个非空值:
a[1][2] = 1; // 1 2 1 刚好是稀疏数组第二行的值
a[2][4] = 2; // 2 4 2 刚好是稀疏数组第三行的值
2
右侧的数组是 N*3 的数组, 假设为 b. b[0][0] 存储着原数组的行数, b[0][1] 存储着原数组的列数。b[0][3] 存储着原数组的非空值的个数。下边每一行的第一个值是 非空值的第一个索引值, 第二个值是非空值的第二个索引值, 第三个值是非空值。
# Show me code
下面是将原始大量空值数组转换为稀疏数组的代码
public static void main(String argv[]) {
// 实例化左侧的数组
int rawArr[][] = new int[11][11];
rawArr[1][2] = 1;
rawArr[2][34] = 2;
// 为了构建稀疏数组第一行, 同时也为了得到稀疏数组的行数, 需要统计原数组的非空值个数
int num = 0;
for(int[] row : rawArr) {
for(int item : row) {
if(item != 0) {
num++;
}
}
}
int sparseArr[][] = new int[num][3];
sparseArr[0][0] = 11;
sparseArr[0][1] = 11;
sparseArr[0][2] = num;
// line 纪录稀疏数组操作到第几行
int line = 1;
for(int i=0; i<sparseArr[0][0]; i++) {
for(int j=0; j<sparseArr[0][1]; j++) {
if(rawArr[i][j] != 0) {
sparseArr[line][0] = i;
sparseArr[line][1] = j;
sparseArr[line][2] = rawArr[i][j];
line++;
}
}
}
// sparseArr 即为转换后的数组。
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
下面是将稀疏数组转换为原数组的的代码
public static void main(String[] args) {
// 虚构出一个稀疏数组
int[][] sparseArr = {
{11, 11, 2},
{1, 2, 1},
{2, 4, 2}
};
// 开始还原原始数组
int [][] rawArr = new int[sparseArr[0][0]][sparseArr[0][1]];
for(int i=1; i<sparseArr.length; i++) {
rawArr[sparseArr[i][0]][sparseArr[i][1]] = sparseArr[i][2];
}
// rawArr 即为原始数组。
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# 有个锤子用?
用于含有大量相同数据的数组的压缩。如棋盘的保存。
===================================================================
# 队列
# 概述
队列是 FIFO 的数据结构。
# 普通数组队列
普通不可复用数组队列属性值及其含义:
| prop | desc |
|---|---|
| maxSize | 定义队列长度 |
| head | 队列首元素前一个位置指针, default: -1 |
| tail | 队列尾元素指针, default: -1 |
普通不可复用数组队列属性值及其含义:
func | core | desc -|- isEmpty() | (tail == head) ? | 首尾指针是否相遇 ifFull() | (tail == maxSize -1) ? | 尾指针是否到最后一个位置 add(value) | queue(++tail) = value | 先将尾指针向后移, 再赋值 get() | return queue(++head) | 先将头指针向后移, 在返回后移后对应的值。 peek() | return queue(head + 1) | 返回头指针后(首)的值,不动首指针
更多判断逻辑见下队列类:
class ArrayQueue {
private int maxSize; // 队列长度
private int head; // 队列首前一个元素指针
private int tail; // 队列尾部指针
private int[] queue; // 队列
public ArrayQueue(int size) {
maxSize = size;
head = -1;
tail = -1;
queue = new int[maxSize];
}
// 是否为空?
public boolean isEmpty() {
return tail == head;
}
// 是否满 ?
public boolean isFull() {
return tail == maxSize-1;
}
// 向队列尾部添加元素
public void add(int item) {
if(isFull()) {
throw new RuntimeException("Queue is Full.");
}
queue[++tail] = item;
}
// 从队列头部获取元素
public int get() {
if(isEmpty()) {
throw new RuntimeException("Queue is empty");
}
return queue[++head];
}
// 查看队列头部第一个元素
public int peek() {
if(isEmpty()) {
throw new RuntimeException("Queue is empty");
}
return queue[head+1];
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
这是最基础的队列, 存在空间利用率低且只能使用一次的缺点。
# 环形队列
环形队列属性值及其含义: ( 为与普通不可复用队列不同点)
| prop | desc |
|---|---|
| maxSize | 定义队列的长度 |
| head | 队列首元素的指针, 默认为0 |
| tail | 队列尾元素后一个位置的指针, 默认为0 |
环形队列成员方法:
| func | core | desc |
|---|---|---|
| isEmpty() | tail == head ? | 一些解释 |
| isFull() | (tail + 1) % maxSize == head ? | 一些解释 |
| size() | (tail + maxSize - front) % maxSize | 一些解释 |
约定: 环形队列中保留一个位置为空,这个位置位于队尾和队头之间, tail 指针所指位置。
更多判断逻辑见下队列类:
class CircleQueue {
private int maxSize; // 队列长度
private int head; // 队首指针
private int tail; // 队尾后一个位置指针
private int[] queue; // 队列数组
public CircleQueue(int size) {
this.maxSize = size;
this.head = 0;
this.tail = 0;
this.queue = new int[maxSize];
}
public boolean isEmpty() {
return this.head == this.tail;
}
public boolean isFull() {
return (this.tail + 1) % this.maxSize == this.head;
}
public int size() {
return (tail + maxSize - head) % maxSize;
}
public void add(int value) {
if(isFull()) {
throw new RuntimeException("Queue is Full.");
}
queue[this.tail] = value;
this.tail = (this.tail + 1) % this.maxSize;
}
public int get() {
if(isEmptu()) {
throw new RuntimeException("Queue is empty!");
}
int returnVal = queue[this.head];
this.head = (this.head + 1) % this.maxSize
return returnVal;
}
public void show() {
for(int i=front; i<this.size(); i++) {
System.out.println("i: " + i + ", value: " + queue[(this.front + i) % maxSize]);
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
==================================================
# 链表
区别于数组的顺序存储结构,链表采用链式存储结构。
一个简单的单向链表的节点应该包括以下信息: 节点内容 和 指向下一个节点的指针。以下是一个最精简的节点类:
class LinkedListNode {
private int no;
private String name; // 内容
private LinkedListNode next; // 下一节点指针
public LinkedListNode(int no, String name) {
this.no = no;
this.name = name;
}
@Override
public String toString() {
return "no: " + this.no + ", name: " + this.name;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
为了方便使用,应该将链表数据和操作链表的方法封装起来。
class LinkedList {
private LinkedListNode head = new LinkedListNode(0, " "); // 头结点
// add to the end
public add(LinkedListNode node)
{
LinkedListNode temp = head;
while(true) {
if(temp.next == null) {
break; // 如果temp移到最后一个位置, 跳出循环添加节点。
}
temp = temp.next;
}
temp.next = node;
}
// add to linkedlist order by no
public void addByOrder(LinkedListNode) {
LinkedListNode temp = head;
boolean flag = false; // 标记是否存在相同 no 的节点, 默认不存在
while(true) {
if(temp.next = null) {
break;
}
if(temp.next.no > node.no) {
flag = true;
break;
}
temp = temp.next;
}
if(flag) {
node.next = temp.next;
temp.next = node;
}else {
temp.next = node;
}
}
// update LinkedListNode by no
public void update(LinkedListNode node) {
if(head.next == null) {
System.out.println("LinkedList is empty.");
return;
}
LinkedListNode temp = head.next;
boolean flag = false; // 标记是否执行修改,默认为false
while(true) {
if(temp == null) {
break;
}
if(temp.no == no) {
flag = true;
break;
}
temp = temp.next;
}
if(flag) {
temp.name = node.name;
}else {
System.out.println("Node do not exists.");
}
}
// delete Node by no
public void delete(int no) {
LinkedListNode temp = head;
boolean flag = false; // 删除节点是佛存在, 默认不存在。
while(true) {
if(temp.next = null) {
break;
}
if(temp.next.no == no) {
flag = true;
break;
}
temp = temp.next;
}
if(flag) {
temp.next = temp.next.next;
}else {
System.out.println("Node do not exists.");
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
# 关于 flag 的作用
在删除、增加、更新中都有 flag 变量,首先要理解的是 while(true) 循环只是为了定位到要操作元素, 真正的操作元素的动作发生在 while(true) 外, 而在循环内部的情况只能通过 flag 反应出来。最佳的编码方式是在 while(true) 外编写操作链表的代码。
# 关于 temp 变量的赋值问题
在单向链表的几种操作中, temp 变量初始值有时是 head, 有的时候是 head.next。这两个变量的选择主要取决于 要进行的操作是否与前节点相关联。
- 增加到末尾,需要前节点的 next 域指向新增节点, 所以 temp = head;
- 按顺序添加, 同上需要前节点的 next 域指向新节点, 所以 temp = head;
- 删除节点, 需要前节点 next 域指向下个节点, 所以 temp = head;
- 更新节点, 只需要关注当前节点, 所以 temp = head.next;
双向链表
双向链表与单项链表的不同点:
- 双向链表相邻的两个节点有两种关联关系: a.next = b; b.pre = a
- 双向链表操作不需要前节点辅助
双向链表的几种操作:
- 增加到末尾: 定位到最后一个元素, tail.next = node; node.pre = tail
- 按顺序添加: 定位好位置, (原来顺序:a.next = b) node.next = a.next; a.next.pre = node; node.pre = a; a.next = node;
- 更新: temp.xxx = node.xxx
- 删除: temp.pre.next = temp.next; if(temp.next != null) temp.next.pre = temp.prei
双向链表节点的最简单结构:
class HeroNode2 {
public int no;
public String name;
public String nickname;
public HeroNode2 pre;
public HeroNode2 next;
public HeroNode2(int no, String name, String nickname) {
this.no = no;
this.name = name;
this.nickname = nickname;
}
@Override
public String toString() {
return "[ no=" + this.no + ", name=" + this.name + ",nickname=" + this.nickname + "]";
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
双向链表类:
class NodeManager {
public HeroNode2 head = new HeroNode2(0," "," ");
public void add(HeroNode2 node) {
// 找到最后一个节点,然后添加即可
HeroNode2 temp = head;
while(true) {
if(temp.next == null) {
break; // 当前temp指向最后一个节点
}
temp = temp.next;
}
temp.next = node;
}
public void addByOrder(HeroNode2 node) {
HeroNode2 temp = head;
boolean flag = false; // 用于标记是否存在 no 相同节点
while(true) {
if(temp.next == null) {
break;
}
if(temp.next.no > node.no) {
break;
}else if(temp.next.no == node.no) {
flag = true;
break;
}
temp = temp.next;
}
if(!flag) {
temp.next.pre = node;
node.next = temp.next;
temp.next = node;
node.pre = temp;
} else {
System.out.println("存在相同的节点");
}
}
public void delete(HeroNode2 node) {
HeroNode2 temp = head.next;
boolean flag = false; // 是否执行了删除,默认未执行
while(true) {
if(temp == null) {
break;
}
if(temp.no == node.no) {
flag = true;
break;
}
temp = temp.next;
}
if(flag) {
temp.pre.next = temp.next;
// 如果是最后一个节点就不需要操作后节点
if(temp.next != null) {
temp.next.pre = temp.pre;
}
System.out.println("成功删除节点:[no=" + node.no + "]");
} else {
System.out.println("未能找到对应节点用于删除");
}
}
public void update(HeroNode2 node) {
HeroNode2 temp = head.next;
boolean flag = false; // 用于标记是否修改,默认未修改
while(true) {
if(temp == null) {
break;
}
if(temp.no == node.no) {
flag = true;
break;
}
temp = temp.next;
}
if(flag) {
temp.name = node.name;
temp.nickname = node.nickname;
}else {
System.out.println("未能找到对应节点");
}
}
public void list() {
HeroNode2 temp = head.next;
while(true) {
if(temp == null) {
break;
}
System.out.println(temp);
temp = temp.next;
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
单向环形链表
最简单的单向环形节点类:
class Node {
private int no;
private Node next;
public Node(int no) {
this.no = no;
}
public setNext(Node node) {
this.next = node;
}
public Node getNext() {
return this.next;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# 环形链表及约瑟夫问题的解决
主要包含了 addToCircle() 用于生成环形链表, show() 用于显示环形链表 , Josephus() 用于处理约瑟夫问题。
class CircleManager {
private Node first = null;
public void addToCircle(int nums) {
// 辅助指针 cursor
Node cursor = null;
for(int i=1; i<=nums; i++) {
Node node = new Node(i);
// 首节点特殊处理
if(i ==1) {
first = node;
cursor = node;
first.setNext(first);
} else {
// 偏好先设置下一节点为头结点
node.setNext(first);
cursor.setNext(node);
cursor = cursor.getNext();
}
}
}
public void show() {
// 空则直接返回
if(first == null) {
System.out.println("链表为空!");
return;
}
Node cursor = first;
while(true) {
System.out.println(cursor);
if(cursor.getNext() == first) {
break;
}
cursor = cursor.getNext();
}
}
/**
*
* @param startNo 起始编号
* @param k 间隔长度
* @param nums 环形链表长度
*/
public void Josephus(int startNo, int k, int nums) {
// 验证参数正确性
if(startNo < 0 || k < 0 || nums < 0) {
System.out.println("错误参数!");
return;
}
//生成环形链表
this.addToCircle(nums);
// 生成辅助指针 cursor 指向 first 前一个节点
Node cursor = first;
while(true) {
if(cursor.getNext() == first) {
break;
}
cursor = cursor.getNext();
}
// 将cursor, first 向后移动 k 位(k % nums)
for(int i=0; i< k%nums - 1; i++) {
cursor = cursor.getNext();
first = first.getNext();
}
// 开始删减环形链表, 直到只剩一个节点( cursor == first)
while(true) {
if(cursor == first) {
break;
}
for(int i=0; i<k; i++) {
first = first.getNext();
cursor = cursor.getNext();
}
System.out.println("删除节点: " + first);
first = first.getNext();
cursor.setNext(first);
}
System.out.println("最后节点是: " + cursor);
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
===================================================================
# 栈 (Stack)
栈是一种先进后出的数据结构(FILO)。 只能在栈的一段进行增加和删除操作,可以操作的这一端称为 栈顶(top), 与之相对的另一端称为 栈底。栈常应用于 子程序的调用、递归的调用、逆波兰表达式等等。 可以通过数组和链表实现栈的结构。
# 通过数组实现栈
数组栈类应该包含的属性及意义。
| prop | desc |
|---|---|
| maxSize | 队列的最大长度 |
| Stack | 队列数组 |
| cursor | 辅助指针,指向栈顶, default: -1 |
数组栈类成员方法列表:
| func | core | desc |
|---|---|---|
| boolean isFull() | (cursor == maxSize -1) | 辅助指针指向最后一个元素为满 |
| boolean isEmpty() | (curosr == -1)? | cursor默认值为-1,也是为空的状态值 |
| void push(val) | stack[++cursor] = val | 指针后移后操作后移的位置,要先判断是否为满 |
| val pop() | return stack[cursor--] | 返回值后,指针前移 |
| void list() | stack[cursorR--] | 利用额外辅助指针遍历 |
附上栈的数组实现代码:
class Stack {
private int maxSize;
private int[] stack;
private int cursor;
public Stack(int size) {
this.maxSize = size;
this.stack = new int[maxSize];
this.cursor = -1;
}
public boolean isFull() {
return cursor == maxSize - 1;
}
public boolean isEmpty() {
return cursor == -1;
}
public void push(int val) {
if(isFull()) {
System.out.println("Stack is full!");
return;
}
stack[++cursor] = val;
}
public int pop() {
if(isEmpty()) {
throw new RuntimeException("Stack is empty.");
}
return stack[cursor--];
}
public void list() {
if(isEmpty()) {
System.out.println("Stack is empty.");
return;
}
int cursorR = cursor;
while(true) {
if(cursorR == -1) {
break;
}
System.out.println(stack[cursorR--]);
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
# 通过 链表实现栈
链表栈应有的属性值:
| prop | desc |
|---|---|
| a | a |
链表栈应有的成员方法:
class ListStack {
private StackNode cursor = new StackNode(0);
private int maxSize;
public ListStack(int size) {
this.maxSize = size;
}
public boolean isEmpty() {
return cursor.getNext() == null;
}
public boolean isFull() {
return cursor.getNo() == this.maxSize;
}
public void push(int val) {
if(isFull()) {
System.out.println("Stack is Full");
return;
}
StackNode node = new StackNode(cursor.getNo() + 1);
node.setVal(val);
node.setNext(cursor);
cursor = node;
}
public int pop() {
if(isEmpty()) {
throw new RuntimeException("Stack is empty");
}
int tmp = cursor.getVal();
cursor = cursor.getNext();
return tmp;
}
public void list()
{
if(isEmpty()){
System.out.println("Stack is empty");
return;
}
StackNode fakeCursor = cursor;
while(true) {
if(fakeCursor.getNext() == null) {
break;
}
System.out.println(fakeCursor.getVal());
fakeCursor = fakeCursor.getNext();
}
}
}
class StackNode {
private int no;
private int val;
private StackNode next;
public StackNode(int no) {
this.no = no;
this.val = val;
}
public void setVal(int val) {
this.val = val;
}
public int getVal() {
return this.val;
}
public int getNo() {
return this.no;
}
public void setNext(StackNode node) {
this.next = node;
}
public StackNode getNext() {
return this.next;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
# 通过中缀表达式来计算多项式
通过栈的数据结构可以实现计算类似于 3+20*4-6/3 这样的表达式。中缀表达式的操作步骤如下:
- 首先,准备两个栈,一个数栈用于存放多项式中的数,另一个存放多项式中的操作符。
- 从表达式左侧挨个字符读入数据, 如果是数则直接入数栈。
- 如果是读取的字符是操作符,当操作栈为空时直接入栈; 当不为空时,1.当读取的操作符的优先级大于操作栈栈顶操作符的优先级,则直接入栈, 2. 当读取的操作符优先级小于或者等于栈顶的操作符优先级, 则将栈顶的操作符弹出记为
oper, 再按顺序从数栈中弹出num1和num2(注意顺序,先弹出的是 num1, 紧接着是num2), 然后计算num2 oper num1的结果入数栈,然后再将操作符入操作栈,此时不用再比较操作符优先级问题。( 但是也可以继续循环操作,直到操作栈栈顶优先级小于操作符优先级,这种做法会节省栈的容量). - 当表达式读取完毕, 数栈和操作栈会有一些数据。循环从操作栈中取运算符,计算数栈栈顶的两个数,直到操作栈为空时计算结束。
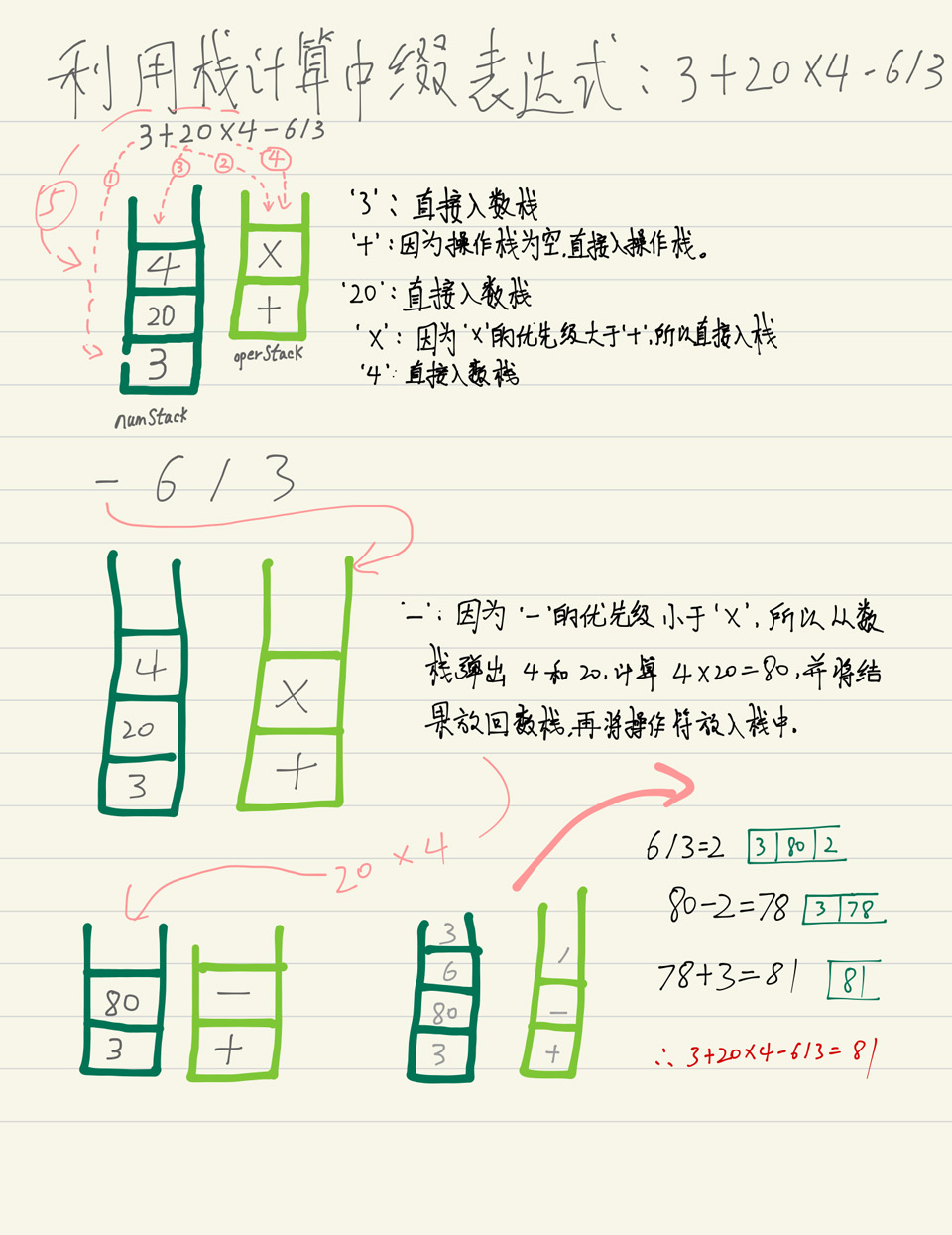
利用栈直接计算中缀表达式:
public class Calcltor {
public static void main(String[] argv) {
String expression = "1+3*2+5-1";
Stack numStack = new Stack(10);
Stack opeStack = new Stack(10);
int num1 = 0;
int num2 = 0;
char ch;
int oper; // 容易写成 char
int index = 0;
String number; // 非个位数存储变量
while(true) {
ch = expression.substring(index, index+1).charAt(0);
if(numStack.isOper(ch)) {
// 如果字符是操作符
if(opeStack.isEmpty()) {
opeStack.push(ch);
} else {
if(opeStack.priority(ch) <= opeStack.priority(opeStack.peek())) {
num1 = numStack.pop();
num2 = numStack.pop();
oper = opeStack.pop();
numStack.push(numStack.calc(num1, num2, oper));
}
opeStack.push(ch);
}
} else {
// 如果是数字, 对多位数进行处理
// numStack.push(ch - 48); 如果计算的是个位数,用这一行即可
number += ch;
if(index == expression.length() -1) {
// 如果是最后一个数
numStack.push(Integer.parseInt(number));
} else {
if(opeStack.isOper(expression.substring(index+1, index + 2).charAt(0))) {
numStack.push(Integer.parseInt(number));
number = "";
}
}
}
if(index == expression.length() -1) {
break;
}
index++;
}
// 处理栈内数据
while(true) {
if(opeStack.isEmpty()) {
break;
}
num1 = numStack.pop();
num2 = numStack.pop();
oper = opeStack.pop();
numStack.push(numStack.calc(num1, num2, oper));
}
System.out.println(expression + "=" + numStack.pop());
}
}
class Stack {
private int maxSize;
private int[] stack;
private int cursor;
public Stack(int size) {
this.maxSize = size;
this.stack = new int[maxSize];
this.cursor = -1;
}
public boolean isEmpty() {
return this.cursor == -1;
}
public boolean isFull() {
return this.cursor == this.maxSize -1;
}
public void push(int val) {
if(isFull()) {
throw new RuntimeException("Stack is full!");
}
this.stack[++this.cursor] = val;
}
public int pop() {
if(isEmpty()) {
throw new RuntimeException("Stack is empty");
}
return this.stack[this.cursor--];
}
public int peek() {
if(isEmpty()) {
throw new RuntimeException("Stack is empty");
}
return this.stack[this.cursor];
}
public boolean isOper(char ch) {
return ch == '+' || ch == '-' || ch == '*' || ch == '/';
}
public int priority(int oper) {
if(oper == '*' || oper == '/') {
return 1;
} else {
return 0;
}
}
public int calc(int num1, int num2, int oper) {
int res = 0;
switch(oper) {
case '+':
res = num1 + num2;
break;
case '-':
res = num2 - num1;
break;
case '*':
res = num1 * num2;
break;
case '/':
res = num2 / num1;
}
return res;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
说明:
上述代码中数栈和操作栈所用的栈类型相同,都是 int 类型, char 数据直接写入 int 是可行的(会自动转为ASCII表中对应的值), 但是将 int 类型数据返回给 char 确实不可行的。!!!
# 后缀表达式的计算及中缀表达式转后缀表达式的方法
后缀表达式就是运算符在操作数后边的表达式。例如 (3+4)x5-6 的后缀表达式就是 3 4 + 5 x 6 -。后缀表达式又叫逆波兰表达式,波兰表达式是前缀表达式的昵称。后缀表达式的计算比较简单,首先1. 从左向右扫描表达式;2.遇到数压入数栈,遇到操作符则从数栈按次序弹出num1 和 num2, 然后计算 num2 运算符 num1 ,并将结果压入数栈。
下边是代码实现计算后缀表达式:
import java.util.Stack;
public class SuffixCal {
public static void main(String[] argv) {
String expression = "3 4 + 5 x 6 -"; // 空格隔开方便操作
String[] list = expression.split(" ");
Stack<String> ss = new Stack<String> (); // 字符串栈
int num1;
int num2;
for(String item : list) {
if(isOper(item)) {
num1 = Integer.parseInt(ss.pop());
num2 = Integer.parseInt(ss.pop());
ss.push(Integer.toString(calc(num1, num2, item)));
} else {
ss.push(item);
}
}
System.out.println(ss.pop());
}
// 判断是否是计算符
public static boolean isOper(String str) {
return str.equals("+") || str.equals("-") || str.equals("x") || str.equals("/");
}
// 计算
public static int calc(int num1, int num2, String oper) {
int res = 0;
switch(oper) {
case "+":
res = num1 + num2;
break;
case "-":
res = num2 - num1;
break;
case "x" :
res = num2 * num1;
break;
case "/":
res = num2 / num1;
break;
}
return res;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
后缀表达式计算相比于之前的中缀表达式计算简便了很多, 下边讨论如何将 中缀表达式转为后缀表达式~
# 中缀表达式转后缀表达式的规则
准备一个运算符栈 S1 和一个操作符栈 S2.
从左向右扫描中缀表达式, 如果遇到数字, 直接入数栈 S2。
如果遇到操作符,按一下顺序判断:
3.1 S1 为空时, 或者 S1 栈顶为)时,直接入栈。3.2 否则, 如果操作符的优先级大于 S1 栈顶 元素的优先级时, 直接入栈。
3.3 否则,将 S1 栈顶的元素弹出并压入数栈 S2, 在将操作符与栈顶元素比较, 重复 3.2 ~3.3 直到操作符入栈。
遇到括号时:
4.1 如果是
(时,则直接入栈 S1.4.2 如果是
), 从运算符栈 S1中弹出元素压入数栈 S2 中,直到遇到(, 弹出(并将这对()舍弃。重复 2-4, 直到扫描完毕。
将 数栈S2 中的元素弹出并压入 符号栈S1,然后从S1 中弹出的顺序就是中缀表达式对应的后缀表达式了。
附上转换代码:
public class Translate {
public static void main(String[] argv) {
String expression = "(30+4)*5-6";
Stack<String> numStack = new Stack<String> ();
Stack<String> oprStack = new Stack<String> ();
int index = 0;
String ch;
String number = "";
while(true) {
ch = expression.substring(index, index+1);
if(isOper(ch)){
if(oprStack.isEmpty() || oprStack.peek().equals("(")) {
oprStack.push(ch);
} else {
if(ch.equals(")")){
while(true){
if(oprStack.peek().equals("(")) {
oprStack.pop();
break;
}
numStack.push(oprStack.pop());
}
} else {
while(!oprStack.isEmpty() && priority(ch) <= priority(oprStack.peek())) {
numStack.push(oprStack.pop());
}
oprStack.push(ch);
}
}
}else {
number += ch;
if(index == expression.length() -1) {
numStack.push(number);
}else {
if(isOper(expression.substring(index+1, index+2))) {
numStack.push(number);
number = "";
}
}
}
if(index == expression.length() -1) {
break;
}
index++;
}
numStack.push(oprStack.pop());
System.out.println(numStack);
}
public static boolean isOper(String ch)
{
return ch.equals("+") || ch.equals("-")|| ch.equals("*")|| ch.equals("/") || ch.equals("(") || ch.equals(")");
}
public static int priority(String ch) {
if(ch.equals("/") || ch.equals("*")) {
return 1;
}else {
return 0;
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
之前的规则叙述判断是罗列形式的,和代码的逻辑不太相同。从代码中可以看出: 1. 是否为数字, 2. 栈是否为空/栈顶是否为’(' , 3. 操作符是 ')'时的操作, 4. 优先级操作
if(不是数) {
if(为空 || 栈顶为'(' ) {
push
} else {
if( ch == ')' ) {
xxx;
} else {
比较优先级
}
}
}else {
//是数
}
2
3
4
5
6
7
8
9
10
11
12
13
上面代码的输出为:
[30, 4, +, 5, *, 6, -]
再结合上面的后缀表达式计算方法,多项式的计算功能。这一切,都是基于 栈.
===============================================================
# 递归算法
# 迷宫回溯
public class Recursion002 {
public static void main(String[] args) {
// init arr
int[][] map = new int[8][7];
for(int i=0; i<7; i++) {
map[0][i] = 1;
map[7][i] = 1;
}
for(int i=0; i<8; i++) {
map[i][0] = 1;
map[i][6] = 1;
}
map[3][1] = 1;
map[3][2] = 1;
map[3][3] = 1;
map[3][5] = 1;
setWay(map, 1,1);
arrPrint(map);
}
// 找到路返回true,否则返回false
// map[6][5] 则找到
// 0 表示该店没有走过
// 1 表示墙
// 2 表示通路可以走
// 3 表示该点已经走过但是走不通
// 下 右 上 左
public static boolean setWay(int[][] map, int i, int j) {
if(map[6][5] == 2) {
return true;
} else {
if(map[i][j] == 0) {
map[i][j] = 2;
if(setWay(map, i+1, j)) {
return true;
} else if(setWay(map, i, j+1)) {
return true;
} else if(setWay(map, i-1, j)) {
return true;
} else if(setWay(map, i, j-1)) {
return true;
}else {
map[i][j] = 3;
return false;
}
} else {
return false;
}
}
}
public static void arrPrint(int[][] arr) {
for(int[] line : arr) {
for(int item : line) {
System.out.printf("%d ", item);
}
System.out.println();
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
输出:
1 1 1 1 1 1 1
1 2 0 0 0 0 1
1 2 2 2 2 0 1
1 1 1 1 2 1 1
1 0 0 0 2 0 1
1 0 0 0 2 0 1
1 0 0 0 2 2 1
1 1 1 1 1 1 1
2
3
4
5
6
7
8
# 八皇后问题
package Recursion;
public class Recursion003 {
int max = 8;
int [] array = new int[max];
public static void main(String[] args) {
Recursion003 queue = new Recursion003();
queue.cheak(0);
}
// 编写一个方法,防止第N个皇后
// 特别注意, check是每一次递归时, 进入到check 都有 for(int i=0; i<max;i++), 因此会有回溯
private void cheak(int n) {
if(n == max) { // 8个皇后放好
print();
return;
}
//一次放入皇后,并判断是否冲突
for(int i=0; i<max; i++) {
array[n] = i;
if(judge(n)) {
// 接着放 n+1 Hang 的皇后
cheak(n+1);
}
// 如果冲突, 执行 array[i+1], 即处理同一行的下一列
}
}
private boolean judge(int n) {
for(int i=0; i<n; i++) {
if(array[i] == array[n] || Math.abs(n-i) == Math.abs(array[n] - array[i])) {
return false;
}
}
return true;
}
private void print() {
for(int i = 0; i < array.length; i++) {
System.out.print(array[i] + " ");
}
System.out.println();
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
输出:
0 4 7 5 2 6 1 3
0 5 7 2 6 3 1 4
0 6 3 5 7 1 4 2
0 6 4 7 1 3 5 2
...............
6 3 1 4 7 0 2 5
6 3 1 7 5 0 2 4
6 4 2 0 5 7 1 3
7 1 3 0 6 4 2 5
7 1 4 2 0 6 3 5
7 2 0 5 1 4 6 3
7 3 0 2 5 1 6 4
2
3
4
5
6
7
8
9
10
11
12
13
================================================================
# 排序算法
排序算法可以分为内部排序法(一次性加载所有数据到内存中)和外部排序法(分批次加载到内存中处理).
# 时间复杂度
时间复杂度是程序运行时间和输出数据的规模的关联关系,用O(n)来表示。时间频率 是精准的程序运行次数,用 T(n)来表示。
有以下代码:
int n = 10;
for(int i=0; i<2n; i++) {
for(int j=0; j<n; i++)
{
xxxx;
}
}
2
3
4
5
6
7
上述代码, 当输入数据量为 n 时, 运行次数为 2n^2。 则 T(n) = 2n^2。
时间复杂度可以由时间频度转换而来,转换规则如下:
- 所有常数项用 1 替代。
- 修改后的 T(n) ,只保留最高阶。如 T(n) = n^2 + n => O(n) = n^2
- 去除最高阶的系数。 如 T(n) = 2n^2 => O(n) = n^2
通过上面的转换,即使两个时间频度不同的算法,时间复杂度也可能相同。比如: T(n)=n^2 + 7n + 8 和 T(n)=3n^2 + 2n + 3 的两个时间频度对应的时间复杂度都是 O(n^2).
只要没有循环等复杂结构,那么算法的时间复杂度就是 O(1).
如果时间复杂度为log,那么底数就变得不再重要。有时候为了简便可以直接写成 lgn, 无论底数应该是多少。
常见的时间复杂度排序: O(1) < O(lgn) < O(n) < O(nlogn) < O(n^2) < O(n^3) < O(n^k) < O(2^n)
我们通常讨论算法的最坏时间复杂度。
# 冒泡排序
相邻比较,把最值放最后边
冒泡排序的原理就是,对于长度为 N 的数列。进行 N-1 (最后只剩一个数的循环可以省去) 次整体循环,每次循环后,将参与循环的所有数的最大值放在最后,然后进行下一次循环,将第二大的数放在倒数第二,.......。循环结束后,就会得到一个有序的数列。 如何在每一次循环中获得最大的值: 依次前后比较,将较大的数放在后边,数列循环完后,最大的数就会放在末尾。
时间频度: T(n) = (n) * ((n+1)/2) = 1/2 n^2 + 1/2n => 时间复杂度: O(n) = n^2.
冒泡的优化: 如果某一次循环中, 一次交换都没有进行,那么数列就已经有序了,后边的排序就可以不用执行。
public class BubbleSort {
public static void main(String[] args) {
int[] numList = {5,2,4,6,1,3};
boolean flag = false;
for(int i=0; i < numList.length -1; i++) {
for(int j=0; j< numList.length - 1 - i; j++) {
if(numList[j] > numList[j+1]) {
flag = true;
int tmp = numList[j];
numList[j] = numList[j+1];
numList[j+1] = tmp;
}
}
if(!flag) {
break; // 没有交换,则证明已经有序,直接退出。
} else {
flag = false; // 有交换,将 flag 重置为 false, 为下一次循环使用。
}
}
showList(numList);
}
public static void showList(int[] list)
{
for(int i=0; i<list.length; i++) {
System.out.printf("%d ", list[i]);
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
Output;
1 2 3 4 5 6
# 选择排序
假设第一个最小,向后挨个比较找到最小与第一个互换。
选择排序的原理就是,从 arr[0 ~ length -1]挨个假设为最值, 从假设位置后一个位置到最后,找到比假设位置值小的最小的值与假设位置交换,即可得到有序数列。
时间频度: T(n) = (n-1) * n/2 = 1/2n^2 - 1/2n => 时间复杂度: O(n) = n^2.
选择排序的技巧: 最后的 minIndex 如果和假设位置相同,则不用交换。

public class SelectionSort {
public static void main(String[] args) {
int arr[] = {8, 5, 7, 1, 9, 3};
int minIndex = 0;
for(int i = 0; i < arr.length - 1; i++) {
minIndex = i;
for(int j = i+1; j< arr.length; j++) {
if(arr[j] < arr[minIndex]) {
minIndex = j;
}
}
if(i != minIndex) {
int tmp = arr[i];
arr[i] = arr[minIndex];
arr[minIndex] = tmp;
}
}
showList(arr);
}
public static void showList(int[] arr) {
for(int i=0; i<arr.length; i++) {
System.out.printf("%d ", arr[i]);
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
Output:
1 3 5 7 8 9
# 插入排序
指针遍历数列,指针后移新元素在指针前寻找合适位置,保证指针前都是有序的。
插入排序的原理是,让
Index从 1 遍历到最后 。 数列可以分为[0 ~ index]和[index+1 ~ length]两个部分。每当指针后移,新加入的 arr[index+1] 就要在 [0 ~ index+1 ] 中寻找合适的位置, 插入。当遍历完[1~最后],整个数列就是有序的了。
时间频度: T(n)= (n-1) * n => O(n) = n^2
插入排序如果用 for 循环 嵌套 for 循环边缘元素不好控制, 改用 while 之后出奇地顺利,指针可以伪指向 arr[-1],这样操作就统一了, 不用很多的边缘 if-else 判断。
public static void main(String[] args) {
int arr[] = {6, 5, 3, 1, 8, 7, 2, 4};
for(int i=1; i<arr.length; i++) {
int currentVal = arr[i];
int cursor = i-1;
while(cursor >=0 && currentVal < arr[cursor]) {
arr[cursor+1] = arr[cursor];
cursor--; // 如果cursor==0, 这步操作后 cursor == -1, 用 for 循环不可控, 这是while的好处。
}
arr[cursor+1] = currentVal;
}
System.out.println(Arrays.toString(arr));
}
2
3
4
5
6
7
8
9
10
11
12
13
Output:
[1, 2, 3, 4, 5, 6, 7, 8]
# 希尔排序
希尔排序是插入排序的优化排序算法,由于优化元素距离对应位置过远的问题。对于插入排序而言,新加入的元素寻址(暂且把元素寻找对应位置的过程叫做寻址)是相邻位置比较,如果用
gap来描述相互比较的元素的距离, 则对于插入排序而言:gap=1。 而希尔排序就是 gap 从length/2逐渐折半直到小于1(大于0),在这个过程中,对索引为 0、gap、gap x 2、gap x 3....进行一次插入排序。当 gap 逐渐变小,整个数列的顺序就会趋于有序,不会出现元素距离对应的排序位置过远的情况,直到最后一次 gap = 1, 就进行了一次整体的插入排序,从而达到避免操作次数过多且完成排序的目的。
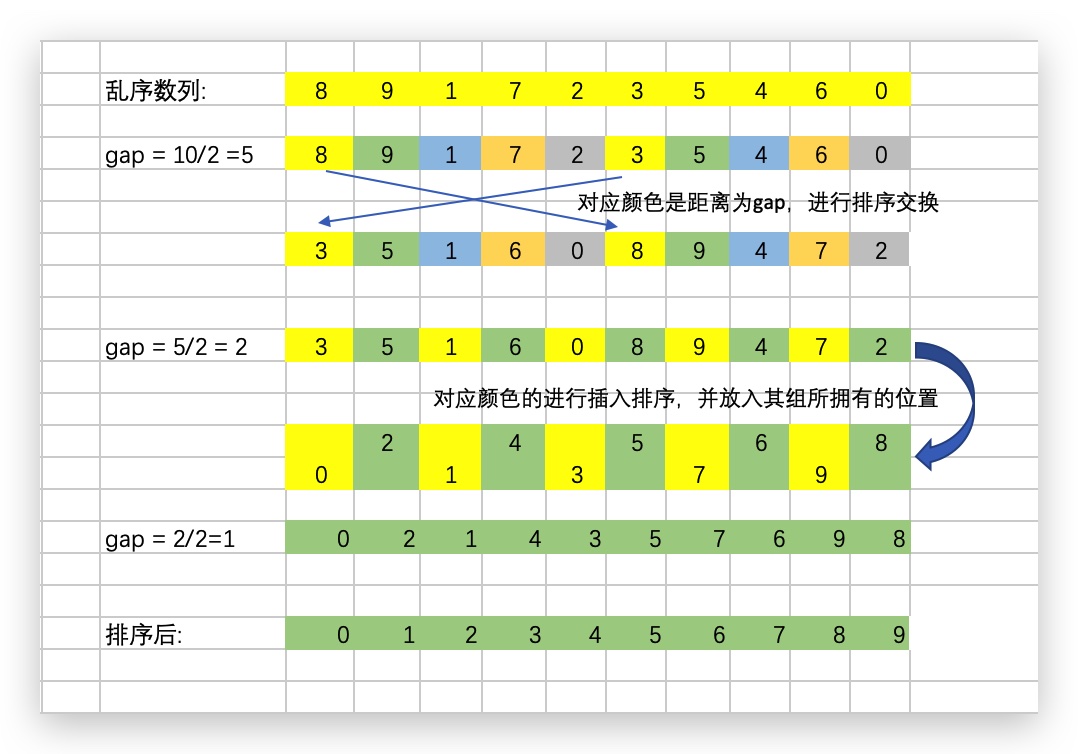
通过 gap 切分的小数列的排序分为两种,一种是挨个比较大小并交换的交换法,另外一种是寻址法,先保留要排序的值,然后将前面的元素后移动,找到合适的位置将保存的值放入即可。
package sort;
import java.util.Arrays;
public class ShellSort {
public static void main(String[] args) {
int[] arr = {8, 9, 1, 7, 2, 3, 5, 4, 6, 0};
shellSort02(arr);
}
// 依次交换的交换法
public static void shellSort(int[] arr) {
int temp = 0;
for(int gap = arr.length/2; gap > 0; gap /= 2) {
for(int i=gap; i< arr.length; i++) {
for(int j=i-gap; j>=0; j-=gap) {
if(arr[j] > arr[j+gap]) {
temp = arr[j];
arr[j] = arr[j+gap];
arr[j+gap] = temp;
}
}
}
}
System.out.println(Arrays.toString(arr));
}
// 使用插入排序的移动法
public static void shellSort02(int[] arr) {
int temp = 0;
for(int gap = arr.length/2; gap > 0; gap /= 2) {
for(int i=gap; i< arr.length; i++) {
int j=i;
temp = arr[j];
if(arr[j] < arr[j-gap]) {
while(j - gap >=0 && temp < arr[j-gap]) {
arr[j] = arr[j-gap];
j-=gap;
}
arr[j] = temp;
}
}
}
System.out.println(Arrays.toString(arr));
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
Output:
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
# 快速排序
快速排序的原理就是找到一个(pivot)作为比较标准,比其小的数放在这个数的左边,比其大的数放在右边。然后以相同的方法处理左边的数列,再处理右边的数列,以此形成递归。最终整个数列就会趋于有序。
这里将数组第一数定为 pivot 讲解。
public class QuickSort {
public static void main(String[] args) {
int [] arr = {4, 10, 8, 7, 6, 5, 3, 12, 14, 2};
sort(arr, 0, arr.length - 1);
System.out.println(Arrays.toString(arr));
}
public static void sort(int[] arr, int lo, int hi)
{
if(lo >= hi) return;
int j = partition(arr, lo, hi);
sort(arr, lo, j-1);
sort(arr, j+1, hi);
}
public static int partition(int[] arr, int lo, int hi)
{
int i = lo, j = hi + 1;
int temp = 0;
int pivot = arr[lo];
while(true)
{
while(arr[++i] < pivot)
if(i == hi)
break;
while(arr[--j] > pivot)
if(j == lo)
break;
if(i >= j)
break;
temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
temp = arr[j];
arr[j] = arr[lo];
arr[lo] = temp;
return j;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
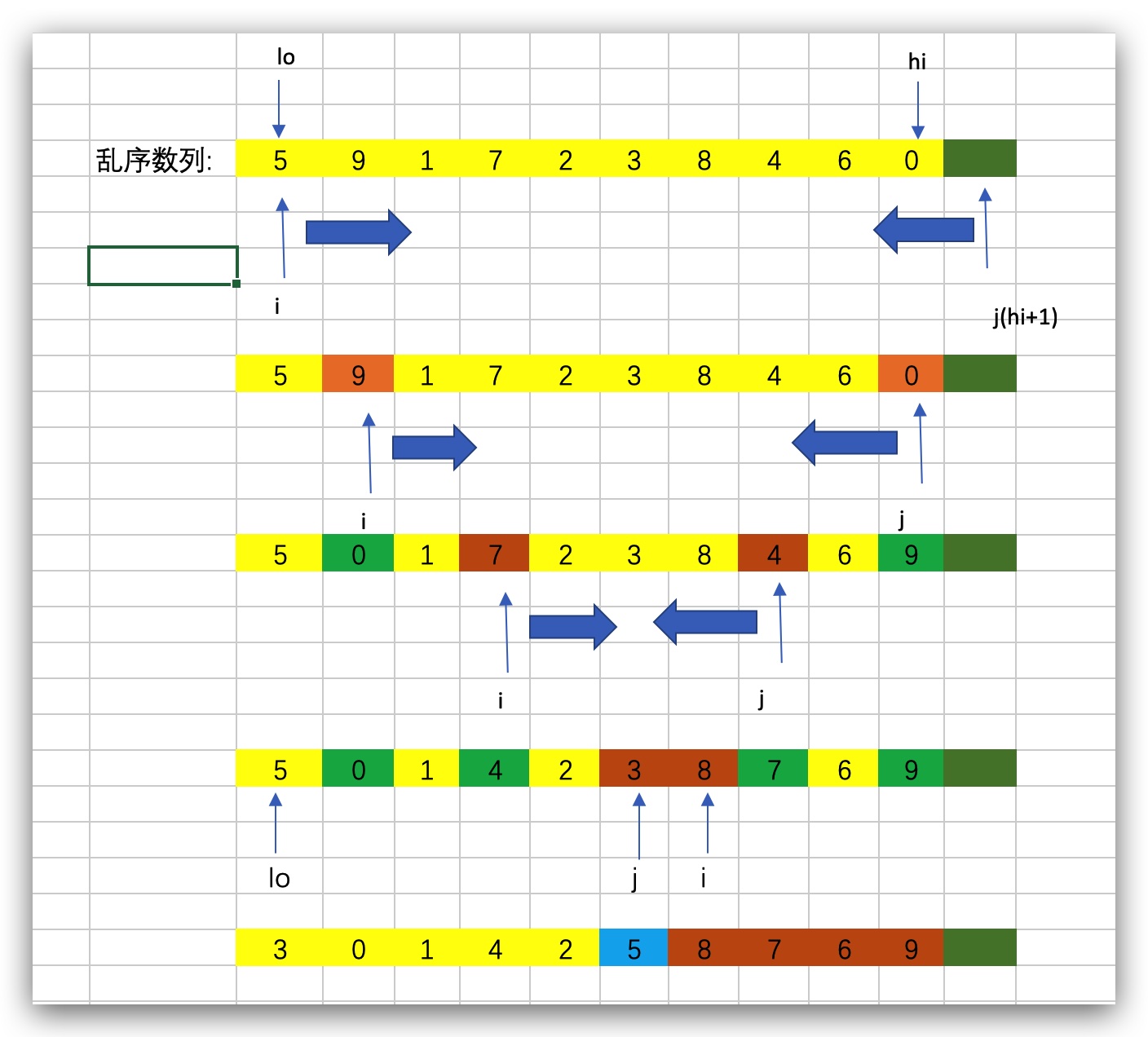
快速排序的算法核心:
会有一个输入的乱序数列, 假设为 arr。定义变量 lo(low) 指向第一个元素, 变量 hi (high) 指向最后一个元素, 这两个元素不能动,用作下次递归的数列边界值。 然后定义 i = lo、 j = hi + 1。 这里解释一下为什么 j = hi +1 ,很是费解的一个问题。【以第一个元素为 pivot 值时, i 实际上是从第二个元素开始后移的, 因为后边第一次调用 i 的形式是 ++i,同理, 因为第一次调用 j 的方式是 - -j, 为了不漏掉尾部元素,只好将 j 赋值为 hi+1 】。
然后指针 i 开始后移,直到遇到大于 divot(5) 的数停止, j 开始前移,遇到小于 divot(5) 的数停止。当 i、 j 确定时, 首先要判断
i、j是否已经到达边界和i 是否大于等于 j。当满足 为到达边界,且 i < j 时,交换指针 i、 j所对应的元素。 图中第二行、第三行都是描述这个过程。如图第四行,当 i<=j 时候, 就不能再交换 i、 j 指针对应的值了。此时应该将 j 指针所对应的值和 divot 交换,得到第五行的结果。如图中所示, 5左侧的值全部小于5, 右侧的值全部大于5.这就是快速排序递归调用中的一个完整案例。
上一步操作中,应该返回 divot 的位置索引 j,用于递归定义下次数据的边界。向递归调用传入边界 (lo, j-1) 和 (j+1, hi)。
递归调用返回条件就是, 当数列小到只有一个元素时(i == j) 则返回。
# 归并排序
归并排序(MergeSort)是一种基于递归的排序算法。先将折半分为两个数列,将两个数列排序后,再将这两个数列通过比较第一个元素大小选择性取出的方式合并为一个数列。而将两个数列排序的方法也是分别将数列拆分为两个数列进行单独排序后再合并。
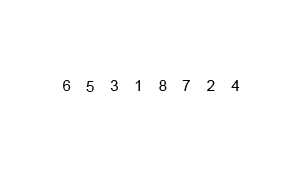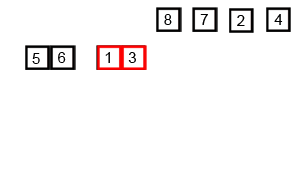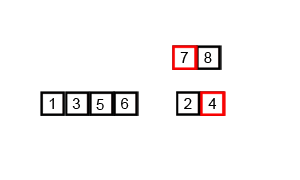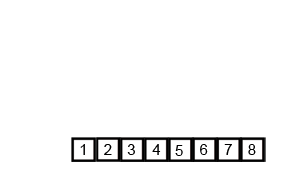
public class MergeSort {
public static int[] aux = new int[8];
public static void main(String[] args) {
int arr[] = {6, 5, 3, 1, 8, 7, 2, 4};
MergeSort(arr, 0, arr.length - 1);
System.out.println(Arrays.toString(arr));
}
public static void MergeSort(int[] arr, int lo, int hi)
{
if(lo == hi)
return;
int mid = (lo + hi) /2;
MergeSort(arr, lo, mid);
MergeSort(arr, mid+1, hi);
Merge(arr, lo, mid, hi);
}
public static void Merge(int[] arr, int lo, int mid, int hi)
{
for(int k=lo; k<=hi; k++)
{
MergeSort.aux[k] = arr[k];
}
int i = lo, j = mid + 1;
for(int k=lo; k<=hi; k++) {
if(i>mid) arr[k] = MergeSort.aux[j++];
else if(j > hi) arr[k] = MergeSort.aux[i++];
else if(MergeSort.aux[i] > MergeSort.aux[j]) arr[k] = MergeSort.aux[j++];
else arr[k] = MergeSort.aux[i++];
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
Output:
[1, 2, 3, 4, 5, 6, 7, 8]
# 基数排序
Magic of Math~ 。
# 基数排序的步骤:
假设排序的数据是: 170, 45, 75, 90, 802, 24, 2, 6
因为数列中最大的数是 170 , 这是一个三位数。所以将所有的数填充到三位:
170, 045, 075, 090, 802, 024, 002, 006
提取个位数,并按照从左到右的顺序根据个位数的大小排序:
170, 045, 075, 090, 802, 024, 002, 006 【原数列】
0, 5, 5, 0, 2, 4, 2, 6 【个位数】
0, 0, 2, 2, 4, 5, 5, 6 【个位数排序】
170, 090, 802, 002, 024, 045, 075, 006 【跟随排序后的数列】
2
3
4
5
提取十位数,并按照从左到右的顺序根据个位数的大小排序:
0, 0, 2, 2, 4, 5, 5, 6 【个位数排序】
170, 090, 802, 002, 024, 045, 075, 006 【跟随排序后的数列】
7, 9, 0, 0, 2, 4, 7, 0 【提取的十位数】
0, 0, 0, 2, 4, 7, 7, 9 【按十位数排序】
802, 002, 006, 024, 045, 170, 075, 090 【跟随排序后的数列】
2
3
4
5
6
提取百位数,并按照从左到右的顺序根据个位数的大小排序:
0, 0, 0, 2, 4, 7, 7, 9 【按十位数排序】
802, 002, 006, 024, 045, 170, 075, 090 【跟随排序后的数列】
8, 0, 0, 0, 0, 1, 0, 0 【提取的百位数】
0, 0, 0, 0, 0, 0, 1, 8 【按百位排序】
002, 006, 024, 045, 075, 090, 170, 802 【跟随排序后的数列】 <---已经是有序数列
2
3
4
5
6
7
# 提取数字小技巧:
个位提取: (num % 10) / 1
十位提取: (num % 100) / 10
百位提取: (num % 1000) / 100
# 代码思路:
假设需要排序 N 个数, 首先需要一个 10N 的二维数组 map ,作为排序的暂存区。 另外需要 110 的一维数组 countArr 来记录 二维数组中每一个一维数组存放的数据个数。
遍历排序数列, 取每一个数的个位数 n , 将 这个数存放到 map[n][countArr[n]++], 一轮过后,将数从二维数组中取出..
按照同样方法处理十位,百位...
最终的数列就是有序的数列。
# 代码实现:
public class RadixSort {
public static void main(String[] args) {
int[] arr = {170, 45, 75, 90, 802, 24, 2, 6};
RadixSort(arr,3);
}
public static void RadixSort(int arr[], int maxLength) {
int[] countArr = new int[10];
int[][] map = new int[10][arr.length];
int num = 0;
// 从个位、十位...遍历每一位
for(int i=0; i<maxLength; i++) {
int index = 0;
// 遍历每一个数
for(int j=0; j< arr.length; j++) {
num = (int)((arr[j] % Math.pow(10, i+1)) / Math.pow(10, i));
map[num][countArr[num]++] = arr[j];
}
// 将数放回 arr
for(int j=0; j<countArr.length; j++) {
for(int k=0; k<countArr[j];k++) {
arr[index++]= map[j][k];
System.out.printf("%d ", map[j][k]);
map[j][k] = 0; //重置countArr/map/index
}
countArr[j] = 0; //重置countArr/map/index
}
index = 0; //重置countArr/map/index
System.out.println();
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
Output:
170 90 802 2 24 45 75 6
802 2 6 24 45 170 75 90
2 6 24 45 75 90 170 802
2
3
# 完结,鸣谢

- 最好懂的快排 (opens new window)
- 最好懂搞得希尔排序 (opens new window)
- 最好懂的归并排序 (opens new window)
- 韩顺平的算法课 (opens new window)
==========================================================================
# 查找算法
# 线性查找
简单暴力缓慢地挨个找。
public class LinerSearch {
public static void main(String[] args) {
int[] arr = {55, 33, 22, 99, 76};
int index = linearSearch(arr, 22);
System.out.println("Target's index is "+ index);
}
public static int linearSearch(int[] arr, int target) {
for(int i=0; i<arr.length; i++) {
if(arr[i] == target) {
return i;
}
}
return -1;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# 二分查找
前置条件: 数列有序。二分查找像极了快速排序,只不过快排需要同时处理 mid 的两遍,而查找只需要寻找一边。
假设在一个从小打大排列的有序数列中寻找一个值,首先寻找有序数列位于中间的值 arr[(hi + lo) / 2], 与寻找的值作比较。如果目标值比中间值大,则在有序数列的右侧部分继续以同样的方法(递归)寻找,反之在有序数列的左侧进行寻值。当最后数列仅剩一个元素 (lo == hi) 时且这个元素不是目标值( arr[lo] != target) 那么久意味着这个数列不存在这个值。

实现代码:
public class BinarySearch {
public static void main(String[] args) {
int[] arr = {0, 4, 7, 10, 14, 23, 45, 47, 53};
int location = binarySearch(arr, 47, 0, 9);
System.out.println(location);
}
public static int binarySearch(int[] arr, int target, int lo, int hi) {
if(lo == hi && arr[hi] != target)
return -1;
int mid = (lo + hi) / 2;
if(target > arr[mid]) {
return binarySearch(arr, target, mid+1, hi);
}else if(target < arr[mid]){
return binarySearch(arr, target, lo, mid-1);
}else {
return mid;
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
Output:
7
# 插值查找
二分查找对比值确定算法。
如果运用二分查找的思想,当我们在一个 1000 页的字典中寻找第900页, 首先是找到中间的第 500 页, 然后是第 750 页,...
显然在日常生活中,我们会往后定位点,第一次可能翻到 800 页或者 950页, 这样查找就会更快些。
插值查找只是优化了中间值的定位, 计算 arr[lo] 与 target 的差值,与 arr[hi] - arr[lo] 的比值, 优化 mid 的定位。具体优化为以下公式:

显然,这种算法的有效性具有“特定情况”才有优化效果:分布均匀的数列才有效。
package search;
public class InsertValueSearch {
public static void main(String[] args) {
int[] arr = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15};
int location = insertValueSearch(arr, 9, 0, 14);
System.out.println(location);
}
public static int insertValueSearch(int[] arr, int target, int lo, int hi) {
if(lo == hi && arr[lo] != target)
return -1;
int mid = lo + (target - arr[lo]) / (arr[hi] - arr[lo]) * (hi - lo);
if(target > arr[mid]) {
return insertValueSearch(arr, target, mid+1, hi);
}else if(target < arr[mid]) {
return insertValueSearch(arr, target, lo, mid -1);
}else {
return mid;
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

